

MATEMATİK TARİHİ
Matematik insanlık tarihinin en eski bilimlerinden biridir. Çok eskiden, Matematik sayıların ve şekillerin ilmi olarak tanımlanırdı. Matematik de, diğer bilim dalları gibi, geçen zaman içinde büyük bir gelişme gösterdi; artık onu bir kaç cümle ile tanımlamak mümkün değildir. Şimdi söyleyeceklerim, matematiği tanımlamaktan çok, onun çeşitli yönlerini vurgulayan sözler olacaktır. Matematik bir yönüyle, resim ve müzik gibi bir sanattır. Matematikçilerin büyük çoğunluğu onu bir sanat olarak icra ederler. Bu açıdan bakınca, yapılan bir işin, geliştirilen bir teorinin, matematik dışında şu ya da bu işe yaraması onları pek ilgilendirmez. Onlar için önemli olan, yapılan işin derinliği, kullanılan yöntemlerin yeniliği, estetik değeri ve matematiğin kendi içinde bir işe yaramasıdır. Matematik, başka bir yönüyle, bir dildir. Eğer bilimin gayesi evreni; evrende olan her şeyi anlamak, onlara hükmetmek ve yönlendirmek ise, bunun için tabiatın kitabını okuyabilmemiz gerekir. Tabiatın kitabı ise, Galile’nin çok atıf alan sözleri ile, matematik dilinde yazılmıştır; onun harfleri geometrinin şekilleridir. Bunları anlamak ve yorumlayabilmek için matematik dilini bilmemiz gerekir. Matematik, başka bir yönüyle de satranç gibi entelektüel bir oyundur.
ÜNLÜ MATEMATİKÇİLER
THALES (İ.Ö. 640-548)
PYHORAS (PİSAGOR) (İ.Ö. 596-500)
ZENO (İ.Ö. 495-435)
DEMOCRITUS (İ.Ö. 470-360)
EUDOXUS (İ.Ö. 408?-355)
ARCHIMEDES (İ.Ö. 287-212)
ÖKLİD (İ.Ö. 300)
APOLLONIUS (İ.Ö. 260?-200? 170?)
HIPPARCHUS (İ.Ö. 160-125)
HAREZMİ (780-850)
GERBERT (945-1003)
ÖMER HAYYAM (1048-1131)
FIBONACCI (1170-1230)
NAPIER (1550-1617)
KEPLER (1571-1630)
DESCARTES (1596-1650)
CAVALIERI (1598-1647)
FERMAT (1601-1665)
PASCAL (1623-1662)
HUYGENS (1629-1695)
GREGORY (1638-1675)
NEWTON (1642-1727)
LEİBNİTZ(1716)


Üslü Sayıları Tanıyalım

Üslü sayılar yandaki şekilde de gösterildiğİ üzere; n tane a sayısının çarpımı a^n ile ifade edilir. Bu ifadeye üslü sayı denir.
Örnekler:
2
3 = 3 . 3 = 9
3
5 = 5 . 5 . 5 = 125
3
(- 2) = (- 2) . (- 2) . (- 2) = - 8
Negatif Üs
Bir tam sayının üssü negatif ise bu sayı rasyonel olarak ifade edilir. Örnek: 2^(-3)= 1 / 8
Rasyonel bir sayının üssü negatif ise verilen rasyonel sayı ters çevrilir.
Örnek: (2 / 3)^(-3)= (3 / 2) 3 = 27 / 8
Üslü sayılarda negatif üssün görevi tabandaki sayıyı ters çevirmektir. Tabandaki sayının işaretini etkilemez
ÜSLÜ SAYILARIN ÖZELLİKLERİ
Sıfır hariç her rasyonel sayının sıfırıncı kuvveti, daima (+1)' dir. Aşağıdaki örnekleri inceleyiniz. Her sayının birinci kuvveti yine kendisine eşittir.
Örnekler:
91 = 9
(-0,5)1 = -0,5
(5/7)1 = 5/7
Rasyonel sayıların üslü sayı olarak yazılması;
Tam sayılı kesirler bileşik kesre çevrilir. Payın kuvveti alınarak paya yazılır. Paydanın kuvveti alınarak paydaya yazılır.
Ondalık kesirlerin üslü olarak yazılması;
(-0,5) . (-0,5). (-0,5) = ( -0,5)^3 = -0,125
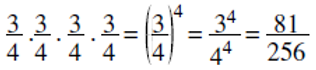
ÜSSÜN ÜSSÜ
Üslü bir sayının tekrar üssü alınırken; Taban aynen yazılır. Üsler çarpılarak tabana üs olarak yazılır. Üsleri çarpanken işaretlere dikkat ederek çarpınız.Yandaki örnekleri inceleyiniz.
